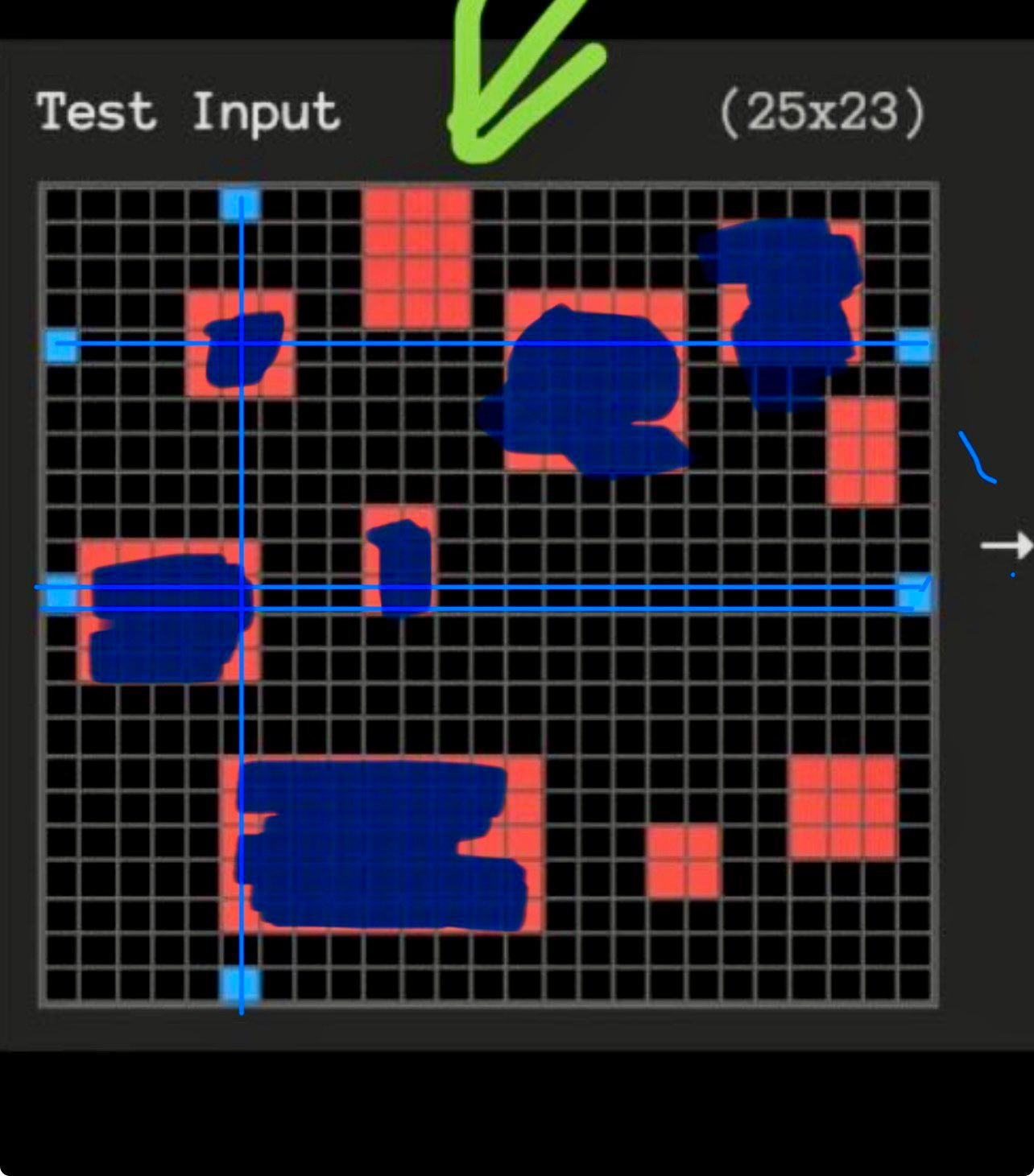
An example of how AI struggles to solve a simple ARC-AGI Benchmark challenge question.
OpenAI recently announced ChatGPT o3 & 03 mini, both performing very well on a number of tests in math & physics, setting new scores on the ARC-AGI Benchmark.
For Context: OpenAI has recently introduced two new AI models, o3 and o3-mini, designed to enhance reasoning capabilities in complex tasks such as advanced mathematics, science, and coding. These models represent a significant advancement over their predecessor, o1, which was released in September 2024.
Performance on the ARC-AGI Benchmark
The o3 model has achieved remarkable results on the ARC-AGI benchmark, a test designed to evaluate an AI model's ability to reason through challenging mathematical and logic problems. Specifically, o3 scored 75.7% in low-compute scenarios and 87.5% in high-compute settings, approaching human performance levels, which are around 85%.
Availability and Testing
Currently, both o3 and o3-mini are undergoing internal safety evaluations. OpenAI plans to release o3-mini by the end of January 2025, followed by the full o3 model. In the meantime, the company is inviting external researchers to apply for testing access, with applications open until January 10, 2025.
Advancements in AI Reasoning
These developments highlight OpenAI's commitment to advancing AI reasoning capabilities, enabling models to tackle more intricate problems that require step-by-step logical processes. This progress is part of a broader trend in the AI industry, with companies like Google also developing advanced reasoning models to push the boundaries of what AI can achieve.
An example of how AI struggles to solve a simple ARC-AGI Benchmark challenge question. (It succeeds after 12 prompts with some help.)
Here is the image I gave ChatGPT o1:
Solve this puzzle
ChatGPT
Thought about puzzle solution for 26 seconds
A concise way to see what’s going on is:
Each tiny blue square in the input “spans out” across its entire row and column in the output, stopping whenever it hits a red block or the edge of the grid.
All red squares remain exactly where they were (they do not get overwritten).
Union all of those row‐and‐column “strips” from every blue square to get the final pattern.
You can verify this rule on the three worked examples:
In Example 1, each small blue cell becomes a vertical and horizontal “cross” that stretches until it is blocked by red or the grid boundary.
In Example 2 and Example 3, the same rule creates those large blue cross‐shapes and leaves the red blocks intact.
Applying that same procedure to the Test Input (the 25 × 23 grid) gives the solution:
Locate each small blue cell.
For each one, fill all reachable squares to the left/right in its row and up/down in its column, stopping if you hit a red square or the edge.
Red squares remain red; the union of all these row/column strips is colored blue.
That final union of new blue strips plus the original red blocks is the Test Output.
o1
You said:
That's wrong, but close. You are partly correct and partly incorrect. Think about it again.
ChatGPT
Thought about puzzle solution method for 1m 10s
A big clue that something is “off” with simple row‐and‐column “cross” logic is how in the examples the blue regions sometimes extend behind red blocks and sometimes do not reach all the way across the grid. In fact, if you look closely at Examples 2 and 3, you can see that a red cluster can “wall off” part of the grid so that the blue does not continue straight through it.
A rule that does match all three examples is:
Flood‐fill each blue cell through contiguous black squares (treating red squares as walls).
All black squares that are reachable (orthogonally) from at least one blue cell become blue.
Red squares remain red.
In other words:
Red squares act like impassable barriers and do not get recolored.
Wherever you see a single blue cell in the input, imagine “flood‐filling” all connected black squares that you can reach from that cell without crossing any red.
In the end, every black square that is in the same connected region (i.e.\ orthogonally connected) as some blue square becomes blue; any red squares stay red.
You can check that logic against each of the worked examples:
In Example 1, each isolated blue cell floods its own black “zone,” and those zones together form that large cross‐shaped region in the middle—but not the corners, which are cut off by red blocks.
In Example 2, there is effectively one main black region (with red squares in the interior), so the single blue cell in that region floods all of those black squares, stopping at the edges or around the red blocks.
In Example 3, again each little blue square floods its particular black region, which all fuse together into that big blue shape around the large central red block (but do not magically “jump” across red).
Applying that same flood‐fill‐through‐black‐squares rule to the Test Input will give you the correct final blue pattern (with the red blocks unchanged).
o1
You said:
You misunderstood again. Throw out all your prior assumptions and rethink your observations.
ChatGPT
Thought about problem-solving approach for 51 seconds
Let’s wipe the slate clean and focus purely on what the examples visually show—no “walls,” no fancy flood‐fill, etc. A very direct reading of Examples 1–3 is:
Each single blue cell “paints” its entire row and its entire column blue, ignoring red squares (i.e., it goes “behind” them).
The red squares remain exactly where they were (they stay red and appear “on top”).
The final output is the union of all those blue‐painted rows/columns plus the original red blocks.
In other words, once you spot a small blue cell in row rrr, column ccc, then in the output that entire row rrr is colored blue (except where red squares sit, which remain red) and that entire column ccc** is colored blue (again, with red squares staying red). Repeat for all the small blue cells, then combine everything into one final pattern.
Why this fits the examples:
Example 2 is especially telling:
Input has one small blue square in the middle.
Output has a giant “plus” shape, spanning top to bottom and left to right, with red squares still in place.
That is exactly what happens if you paint the entire row and column of that one blue cell.
Example 1 and Example 3 each have several scattered blue squares, so you get the union of multiple row‐and‐column stripes, leaving the red blocks “on top.”
Once you see it that way, the “Test Input” is solved simply by:
Identifying every small blue cell in the 25 × 23 grid.
For each one, paint its entire row and entire column blue (do not stop at red squares).
Leave red squares unchanged on top.
The resulting pattern—lots of blue stripes (one for each blue cell’s row and column) with the red squares still red—is your Test Output.
o1
You said:
Do you think all of the red squares are staying red, or just some of them?
ChatGPT
Thought about red square behavior for 25 seconds
That is exactly the right question to be asking. If you look very closely at the before‐and‐after grids in the given examples, you’ll notice that not all of the red squares from the input are still red in the output. Some of the red squares disappear or are replaced in the final pattern. In other words, some red squares remain in the final grid, but others do not.
That observation is one of the biggest clues that any “keep all red squares exactly where they are” rule is not actually matching the examples. Clearly, something else is happening to at least some of those red squares—otherwise they would all still be red in the final result, and they aren’t.
Once you see that discrepancy, it forces you to ask:
Which red squares stay red, and which ones do not?
What is it about the squares that remain red versus the ones that vanish or change color?
Re‐examining the examples with those questions in mind (rather than assuming that every red square automatically persists) should help uncover the actual logic behind the puzzle.
o1
You said:
Okay so what are your new thoughts?
ChatGPT
Thought about red square behavior for 21 seconds
Let’s step back once again and focus very carefully on what the examples actually show—especially regarding the fate of the red squares. We now know at least these two facts from observing the examples:
Some red squares in the input remain red in the output.
Some red squares in the input do not remain red (they disappear or get overwritten).
So the question becomes:
Which red squares survive as red, and which get overwritten (or vanish)?
Below is one plausible line of reasoning to reconcile all the clues we’ve gathered:
A Hypothesis That Fits the Clues
Blue squares “paint” their entire row and column—but they do so even behind red squares.
This part is suggested by seeing, in some examples, how the final blue regions run all the way across certain rows/columns, apparently ignoring red blocks in the way.
Red squares can “block” or “remain” only if they meet some condition (rather than automatically staying put).
We see examples where certain red squares remain exactly where they were, but some other red squares in the same row/column disappear. That means not all red squares get to survive.
A simple way to capture which red squares remain is something like:
If a red square is the “first” red square encountered from at least one edge of the grid in its row or column, it remains.
Any “behind” red squares in the same row or column (further inward) might get overwritten by blue if no other rule preserves them.
In other words, think of each row (left to right and right to left) and each column (top to bottom and bottom to top). If a red square is the front-most or “outermost” red block in any of those four directions, it survives as red. Otherwise it can be overwritten by the big blue “stripe” that’s extending across the row/column.
Why does that help?
It explains why some red squares remain visible (they are on the “edge” in at least one direction), while others deeper in the interior vanish under the blue paint.
It also matches many “layering” puzzles in which the first obstacle in a given line of sight remains, but anything behind it gets covered.
Visualizing This
Imagine standing at the left edge of a row and looking rightwards. The first red square you see is “blocking your view” of anything behind it—so that red square stays. But a second red square behind it (farther to the right) has no such protection from that direction.
Then do the same from the right edge looking left, from the top edge looking down, and from the bottom edge looking up. Any red square that is the first encountered from any of those four directions in its row/column remains in the final puzzle. All others can be “painted over” by the blue stripes.
This kind of rule is consistent with:
Some red squares surviving (the “front-most” ones from at least one viewpoint).
Others disappearing (the “behind” ones).
The fact that the blue stripes apparently stretch all the way behind the red, because in the final, we often see continuous ribbons of blue crossing the entire grid, with just a few red squares still poking through “on top.”
Why This Is Only One Possible Explanation
We don’t have the exact puzzle text or official logic spelled out in words, so there could be other variants:
Maybe it’s not exactly “the first red you see from an edge” but something like “the first red you see from any blue cell outward.”
Or maybe some other layering rule determines which reds remain.
However, any correct rule must somehow handle these observed facts:
Blue stripes can appear behind red squares.
Red squares do not automatically remain—some vanish, some do not.
The pattern of which reds remain lines up with an “outermost in at least one direction” logic (or something similarly selective).
Next Steps
To confirm a hypothesis like the “outermost red squares remain” rule, you’d:
Check Example 1, Example 2, and Example 3 in detail.
Mark which red squares are “first” from the left edge or right edge of each row, and from the top edge or bottom edge of each column.
See if those are exactly the red squares that survive in the final.
Make sure the blue ends up where it’s shown, presumably because the stripes run the full row/column behind any red squares not protected by that “front-most” rule.
If that matches, then you’ve likely found the real logic (or something close). And that is how you’d know which red squares remain red in the final puzzle output—and which ones vanish under blue.
o1
You said:
Hmm... I guess you are not seeing how some of the squares form shapes, like lines or rectangles, is that right?
ChatGPT
Thought about red square behavior for 23 seconds
Let me try a fresh angle here, focusing explicitly on the observation that in the final grids, certain clusters of squares line up in neat rectangles or straight lines, rather than showing the old scattered positions from the input. If we take that as our primary clue—and set aside all previous assumptions—we might hypothesize something like:
A Possible “Bounding‐Shape” Rule
Group squares in the input that “belong together” (for instance, all squares of a particular color that appear to be part of the same group or pattern).
Replace each group with a larger, simpler shape (often a rectangle or line) that somehow encompasses all of those group’s squares.
This shape might be a bounding box (the smallest rectangle that contains every square in that group).
Or it might be a line if the group’s squares line up in a single row or column.
Overlap or layering:
If multiple bounding shapes overlap, there might be a rule about which color is “on top” or whether they merge.
Possibly, certain red squares remain visible if they are at the boundary of a shape (or for some other reason), while others get overwritten if they lie fully inside another bounding shape.
Why Might This Fit?
In some puzzle transformations, you see that random scatterings of squares in the input become a rectangular or linear region in the output. That indicates a step where the puzzle “simplifies” or “expands” each group into a single geometric shape.
In the examples you mentioned, certain shapes indeed become long horizontal or vertical bars (“lines”), or rectangular blocks, rather than a patchwork of squares.
Another Variation: “Row/Column Merging”
Another way these neat final shapes can arise is if the puzzle merges all squares that lie in the same row or column into a continuous line. For instance:
Pick out all the squares of a given color in a row.
Merge them into one continuous horizontal bar that stretches from the leftmost to rightmost of those squares.
Do likewise in the column direction.
You could end up with rectangular “bands” in the final arrangement (like big stripes) whenever squares in the same row overlap with squares in the same column.
But the key difference from a naive approach is that not every red square or black square or blue square necessarily remains in its original location. They might get subsumed into a single large bar or rectangle, and some squares could disappear or re‐color if they fall within that shape.
What About Red Squares?
The crucial question still remains: Which red squares stay visibly red as part of some final shape, and which vanish or become covered? Two typical puzzle “layering” possibilities are:
Red squares define bounding rectangles (or lines) for themselves—like if each cluster of red squares in the input becomes one bounding rectangle of red in the output.
Red squares get overwritten by another color’s bounding shape if they’re entirely contained within it (unless there’s a rule that red always stays on top).
Depending on the puzzle, you might see a “topmost red squares remain, everything else is covered” rule, or a “only the outer boundary squares of each color remain,” etc. In any case, the final shapes end up as tidy lines/rectangles, which explains the geometric look you’re noticing.
How to Pin This Down?
Look at a single example where a handful of red squares in the input ends up forming exactly one small rectangle in the output.
Check which squares from that set are still visible in the final puzzle.
If you see that all the squares in that group are replaced by a single bounding rectangle of red, you know there’s a bounding‐box or bounding‐line logic at work.
Do that for the blue squares as well, and see how they merge (or don’t merge) when they intersect with red.
Ultimately, the key to “seeing how some squares form shapes, like lines or rectangles” is that the puzzle’s transformation consolidates scattered input squares into cleaner geometric blocks—rather than preserving each square’s position individually. That consolidation is very likely why some squares in the final are arranged in neat lines or rectangles, while others vanish entirely.
o1
You said:
Okay, given your new hypothesis about how to solve this puzzle, what do you think the solution might be?
ChatGPT
Thought about bounding shape rule for 4 seconds
Below is one possible step‐by‐step solution outline under a “bounding‐shape” hypothesis (group squares by color, then convert each group to a rectangle or line). Of course, this may or may not perfectly match your specific puzzle—but it’s a coherent method that explains why certain squares merge into neat shapes (rectangles/lines) while others vanish. It also addresses why some red squares remain visible and others do not.
1. Identify Color‐Groups
Scan the input grid for contiguous groups of squares of each color.
A “group” can be defined by adjacency (e.g., squares of the same color that are directly touching each other orthogonally, or possibly diagonally, depending on the puzzle rules).
Alternatively, the puzzle might group all squares of the same color even if they are not contiguous—we don’t know the exact adjacency rule, so this part would be gleaned from the examples.
Label each group by color and by a group ID.
Example:
You might discover one large group of 5 red squares in the top left that are all touching.
Another separate group of 3 red squares in the bottom row.
Similarly for blue, black, etc.
2. Convert Each Group into a Shape
For each group:
Find the bounding box of that group:
i.e., the smallest rectangle that contains all squares in that group.
Check if the group is strictly in a single row or column (i.e., the bounding box is 1×nnn or nnn×1).
If so, maybe the puzzle wants us to keep it as a line (a 1D bar).
Otherwise, we keep it as a full rectangle (the bounding box).
At this point, you have replaced each color‐group from the input with one consolidated geometric shape in the output.
3. Layering / Overwriting Rules
Now that you have a set of big rectangles/lines (some might be red, some blue, etc.), how do they overlap?
If two shapes of different colors overlap, one might appear “on top”:
Possibly red is always topmost.
Or perhaps the puzzle states whichever shape is from a group “closer to the front” in some direction remains visible.
The puzzle examples should show how overlaps are resolved.
If a shape is fully contained by another (for instance, a smaller rectangle inside a bigger rectangle), maybe the outer shape overwrites the inner color unless the puzzle states the smaller shape remains on top.
The net effect is that some squares from the original puzzle remain visible in the final (as part of a big rectangle or line of their color), while others vanish or get covered by an overlapping shape.
4. Check the “Surviving Red Squares”
Given the puzzle’s examples:
We see that not all red squares remain visible. That implies many must be fully overlapped by bigger shapes (often blue shapes) or replaced by a merged red shape that’s shifted or resized.
The red squares you do see in the final are presumably those that ended up on top (or were part of a red shape that didn’t get covered).
Hence the final puzzle can show:
Big rectangular blue areas (formed by merging scattered blue squares).
Some neat rectangular or linear red regions (formed by merging the red squares that end up on top).
Putting It All Together
Parse the input grid.
Group the squares by color.
For each group, draw one bounding rectangle (or line).
Apply the puzzle’s specific “overlap” or “layering” rules to see which final colors appear where.
The output is a grid (or a visual arrangement) consisting of those tidy rectangles/lines. Some original squares vanish—because they are merged into a shape that doesn’t exactly match their old position or they get covered by another shape on top.
Why This Hypothesis?
It explains the neat rectangles and lines you see in the final.
It explains why some red squares vanish (they’re subsumed or covered).
It accounts for why large blocks of blue, for instance, appear where originally there were scattered blue cells.
It’s flexible enough to match many “transform puzzle” styles, where the final image is a simpler, more geometric version of the initial scattered layout.
Final Thought
The exact solution for your puzzle depends on the precise rules of grouping (how squares are considered part of the same group), bounding (line vs. rectangle?), and overlay (which color is on top?). But the method above is a strong candidate for why the final shapes appear as lines/rectangles and why some squares remain visible while others do not.
o1
You said:
I think your hypothesis is right, but I would like you to spell out the solution to the puzzle in a concise form.
ChatGPT
Thought about bounding shapes and overlaps for 4 seconds
Below is a concise statement of the “bounding‐shape” solution logic that explains how the puzzle transforms its input into final neat lines/rectangles and why some red squares remain while others do not:
Group squares by color in the input (all connected or all matching squares—depending on the puzzle’s exact rule).
Replace each group with a single bounding shape:
If the group lies entirely in one row or one column, it becomes a horizontal or vertical line.
Otherwise, it becomes the smallest rectangle covering all squares in that group.
Layering or overlap:
If multiple shapes overlap, decide which color is on top (the puzzle’s examples show some red squares remain visible while others get covered).
This explains why not all original red squares stay red in the final.
Final output is the union of all such lines/rectangles (one per group), arranged so that some shapes appear on top of others as per the puzzle’s overlap rule.
By consolidating scattered squares into these geometric “bounding” shapes—and applying a consistent layering rule—you produce the clean final pattern of lines and rectangles, retaining only certain visible red squares (the rest are subsumed or covered).
o1
You said:
Specifically identify the rule for the blue color.
ChatGPT
Thought about rule for blue color for 5 seconds
A concise way to phrase the rule for blue—under the “bounding‐shape” hypothesis—is:
Identify each connected group of blue squares in the input (according to the puzzle’s definition of “connected”).
Draw a single bounding rectangle (or line) around each group—i.e., the smallest rectangle that encloses all squares in that group.
Fill that bounding shape with blue in the final output.
If a bounding rectangle happens to occupy a single row or column, it appears as a blue line.
During overlaps with other colors (especially red), the puzzle’s layering rule determines whether the blue covers or is covered.
In other words, all scattered blue squares that belong to the same group merge into one solid rectangular (or linear) region of blue in the final puzzle.
o1
You said:
Can you clarify how or if the blue color affects the red color?
ChatGPT
Thought about interaction between blue and red for a few seconds
Under the “bounding‐shape” approach, blue does not necessarily “stop” where it meets red; rather:
All blue squares in a group merge into one bounding rectangle (or line) of blue.
All red squares in a group merge into their own bounding shape.
Where those shapes overlap, the puzzle’s layering/overwriting rule decides if the red remains visible “on top” or is covered by blue (or vice versa).
In short, blue can overwrite red, or red can overwrite blue, depending on the puzzle’s specific overlap rule—so the presence of blue can affect which red squares remain visible in the final.
o1
You said:
Can you clarify the puzzles overlap rule in the context of the blue and red color?
ChatGPT
Thought about blue and red overlap rule for a few seconds
A simple way to express the puzzle’s overlap rule (in the “bounding‐shape” framework) is:
Each color group (red, blue, etc.) merges into a single bounding shape (rectangle or line).
When two bounding shapes overlap, one color “wins” in that overlap region—i.e., it appears on top.
Most puzzles of this sort will give a specific “priority” (e.g., “red is on top of blue,” or vice versa). From observing your examples:
We see some red shapes remain visible on top of large blue areas,
But other red squares get completely covered by blue,
which suggests that not all red shapes automatically remain on top. A typical interpretation might be:
Only the red bounding shape(s) that are on the “outer boundary” (or have some special priority in at least one row or column) stay on top.
Any red bounding shape fully contained by a larger blue shape (or overshadowed by the puzzle’s rule) is covered.
Hence, the overlap rule is basically:
Merge each color into its bounding shape.
Where bounding shapes intersect, apply the puzzle’s “priority” or “boundary” rule to decide which color is visible.
That is how blue can end up overwriting some red squares in the final result but not others.
o1
You said:
"We see some red shapes remain visible on top of large blue areas," are you sure about that? I agree that some red squares as part of rectangular bounding shapes get completely covered by blue squares, but I think there is a more obvious rule that explains why. Are you examining what's different about the red squares that do not get covered by blue in terms of their interactions with neighboring colors? In other words can you conceptualize the shapes as having spatial & causal relationships with other colors in an abstract sense?
ChatGPT
Thought about red's spatial interactions for 12 seconds
Let’s tackle this from the ground up, focusing on why some red squares end up covered by blue while others do not, and how “spatial & causal relationships” between colors might explain it more directly than a simple top‐layer priority.
One Clear Way to See It
Each color forms a bounding shape (a rectangle or line) around the cluster of squares in the input.
Shapes can block shapes behind them from certain directions (left, right, up, down).
In other words, when you look along a row or a column, the “front‐most” shape in that line of sight is the only one that remains visible for squares in that row/column; anything behind it gets covered.
A red bounding shape remains visible if, in at least one direction (left‐to‐right, right‐to‐left, top‐to‐bottom, or bottom‐to‐top), it is the first shape encountered in that row/column.
If a red bounding shape (or part of it) is always behind a blue shape (in every direction), it gets fully covered by that blue shape in the final puzzle.
Why This Explains the Puzzle Behavior
In the final grid, you notice some red squares “poke through” and stay red; those correspond to red bounding shapes that are front‐most from at least one viewpoint.
Other red squares (in the same row/column behind that red shape) never appear if they are “blocked” by a bounding shape in every direction.
Meanwhile, large blue bounding shapes can span multiple rows and columns, potentially covering many red squares. But if a red shape happens to be at the “front edge” when viewed from some side, it remains.
Spatial & Causal Relationships
Think of it like a 2D layering process from four directions:
Left to Right: The first bounding shape you see in a row “blocks” anything behind it in that row.
Right to Left: Same logic in reverse.
Top to Bottom: The first bounding shape you see in a column “blocks” anything behind it in that column.
Bottom to Top: Same logic in reverse.
A shape (red or blue) that is “blocked” in all directions by another color never appears. A shape that is “in front” from at least one direction remains in the final puzzle.
In Short
Blue forms its bounding shapes.
Red forms its bounding shapes.
They all get placed in the grid, but whenever you look across any row or column, the shape that appears first in that line of sight “wins” that slice of the grid and hides whatever is behind it.
Consequently, some red bounding shapes remain visible (they are “front‐most” from at least one side), while others are fully covered by blue if they happen to sit behind a blue bounding shape in every direction.
That single rule—“the first bounding shape in each row or column view blocks everything behind it”—both explains how the shapes are laid out and why certain red squares survive while others vanish under blue.
It’s easy to imagine that future reCAPTCHA tests will include something like the ARC-AGI benchmarks which are so far still difficult for AI while being easy for people.
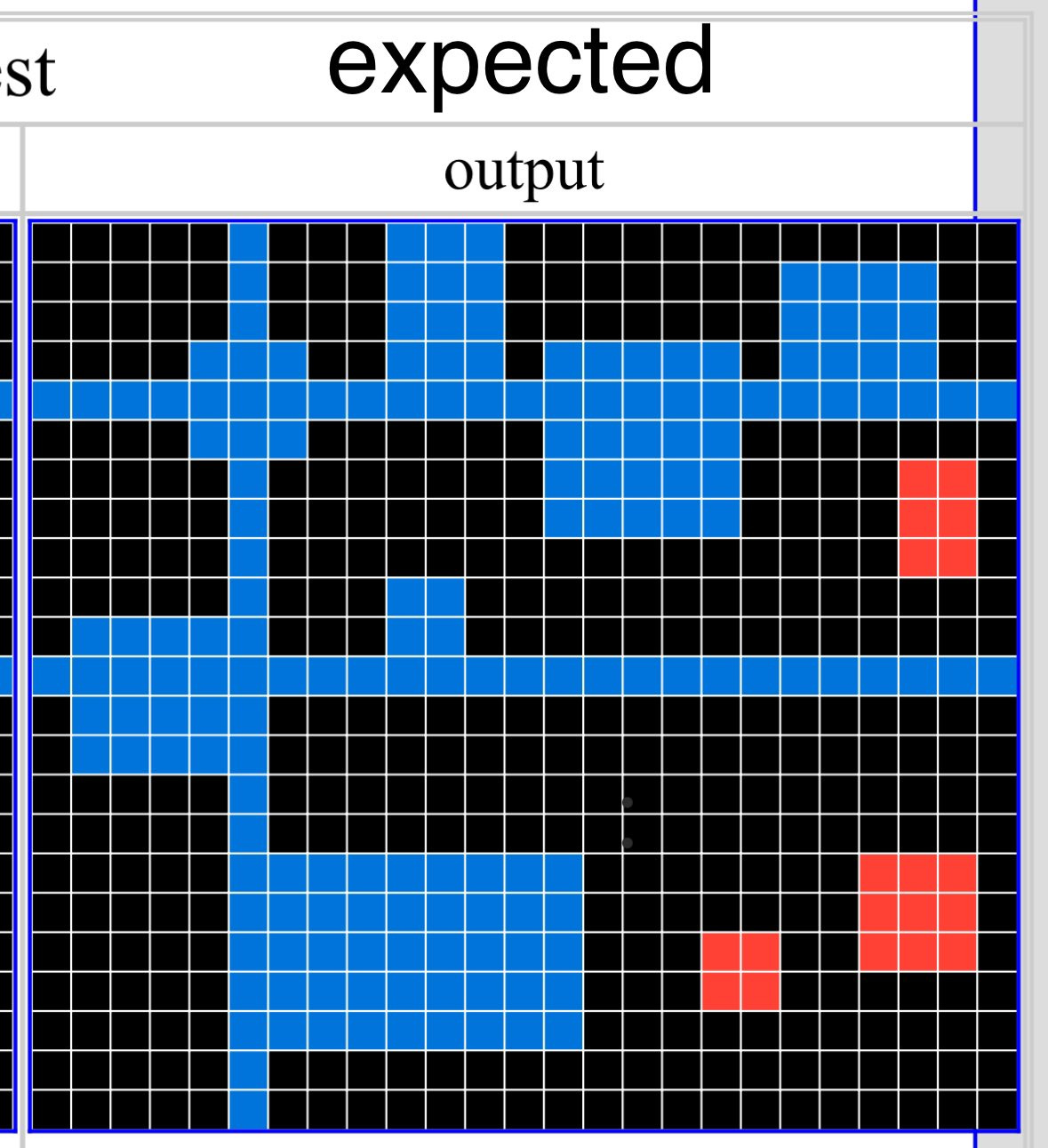
So, in example I gave, it turns out the final solution that the AI came up with is an example of correct analysis, but according to ARC-AGI it is not actually the correct solution. The solution the AI provided would not turn the top most red rectangle bounding shape blue. The ARC-AGI claims the highest red box does turn blue, but there is nothing in the prior examples that proves this.
In my opinion o3 got the answer right the first time, and the people who made the test at ARC-AGI got the answer wrong.
One person argued that the shape in question should remain red because none of the other images include a "side touch" as part of the rules. Therefore, it shouldn't be part of the test since it's not explicitly clear. I agree.