TDF-0 vs. Super Information Theory (SIT): a translation map, distinguishing test, and precedence timeline

A comparative analysis of the work of Joshua Thompson (TDF-0) and Micah Blumberg (SIT) reveals significant conceptual overlap in their approaches to fundamental physics.

A comparative analysis of the physics work of Joshua Thompson “Thompson Dimensional Framework Origin (TDF-0)” and Micah Blumberg’s “Super Information Theory (SIT)” reveals significant conceptual overlap in their approaches to fundamental physics. Both aim to derive physical laws from a deeper information-theoretic or computational substrate. This analysis will decode key phrases and mathematical concepts from both authors' works, present a compact translation map from TDF-0 observables to SIT fields, and note a simple distinguishing test, highlight the substantial overlap, and provide a timeline that anchors priority by public timestamps.

Core overlap at a glance

• Origin from minimal primitives. TDF-0’s “zero-import” origin matches SIT’s information-first substrate with operational fields: the coherence field ψ(x)=√(R_coh(x))·e^{iθ(x)} and the time-density field ρₜ(x).

• Single generator → many laws. TDF-0: a recursion over 35 operators and a dimension-scaling factor Ω_D=((D−2)/2)^λ with worldsheets. SIT: a unified action where informational fields source gravity and electromagnetism (A_μ=(ℏ/e)·∂_μθ).

• Emergent structure and constants. Both claim sector laws and effective constants emerge internally (SIT with explicit gauge-holonomy and metrology predictions; TDF-0 with Ω_D, Polyakov worldsheets, and c=D).

---

Thompson Dimensional Framework Origin (TDF-0)

Joshua Thompson’s TDF-0 is a theoretical framework that aims to generate the laws of physics from a state of “absolutely no predefined structure or physical assumptions.” Key features:

• Zero-Import Framework. TDF-0 is described as a “zero-input, entropy-driven, self-originating mathematical framework” that generates space, time, physical constants, and field structure from a uniform substrate with purely local rules.

• Emergence of Laws and Constants. The text claims spontaneous emergence of dimensionless analogues of constants (ℏ′, G′, α′, Λ′) and symmetry shells mirroring U(1), SU(2), SU(3), arising from internal recursion rather than assumed laws.

• Recursive/Iterative Engine. A closed set of 35 recursive operators (Δₖ) acts on an initial near-void field, with additional patch operators Δ′ introduced to fix failure modes—still within the internal logic.

• Scaling and Worldsheets. A unique dimension-scaling factor Ω_D = ((D−2)/2)^λ (λ>0) and a Polyakov worldsheet with tension T_D = Ω_D·T₀ (central charge c = D) are derived at coarse-grained level; D = 2 is shown as a nonlinear repellor.

Micah Blumberg's Work (SIT, SDT, QGTCD)

Micah Blumberg’s Super Information Theory (SIT) presents a framework for deriving physics from an information-first substrate. Key elements:

• Information as Substrate. SIT postulates a complex coherence field ψ(x) with phase θ(x) and a real time-density field ρₜ(x); information is operationally tied to local coincidence events.

• Unified Action. A single covariant action governs ψ and ρₜ, with gravity and electromagnetism emerging from informational geometry; EM arises from phase holonomy A_μ = (ℏ/e)∂_μθ.

• Core Fields. Coherence ratio R_coh(x) ≡ |ψ(x)| (order) and time-density ρₜ(x) (event/clock rate) serve as primitives.

---

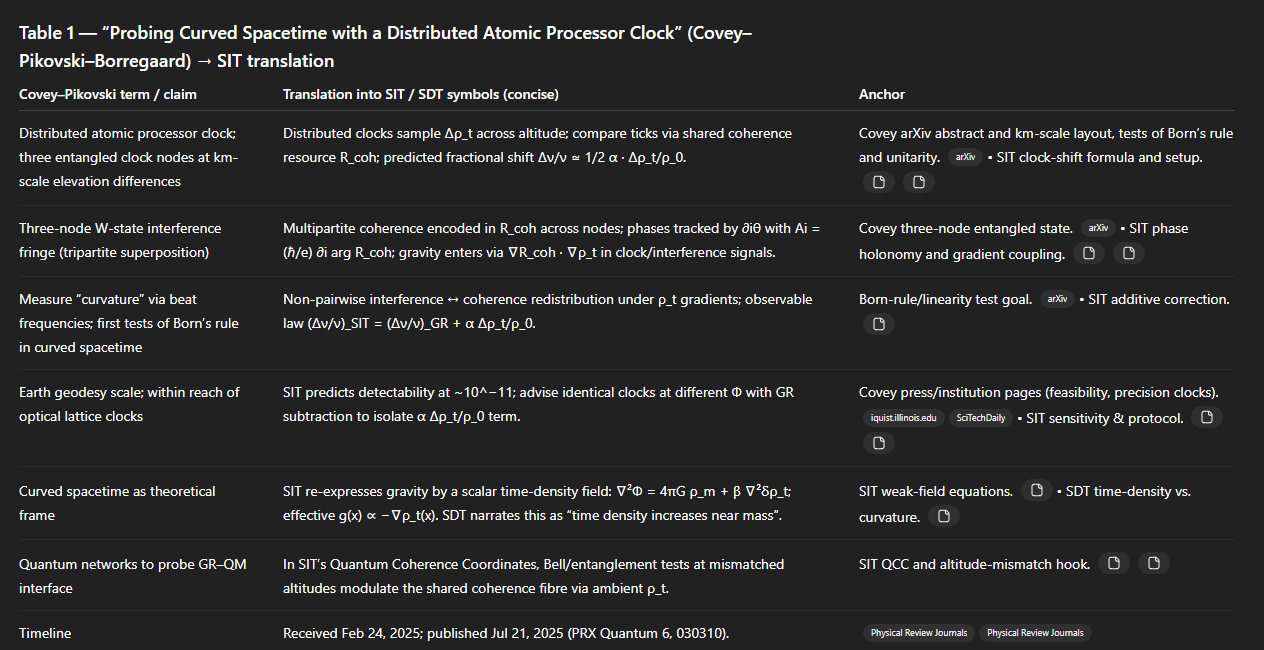
The Formal Translation Map: ⟦TDF⟧ → SIT

An explicit operational encoding, ⟦TDF⟧, can be defined to translate the coarse-grained observables of any Thompson Dimensional Framework (TDF) history into the physical fields and dynamics of Super Information Theory (SIT). This map reveals the deep structural and conceptual equivalence between the two frameworks.

1. Time-Density (ρₜ) from Event Rate

The SIT time-density field, ρₜ(x), is derived from the rate of TDF's computational events. For any spacetime region Ω, let N_front(Ω) be the count of TDF's active boundary updates. The operational definition is then the local density of these events per unit of proper time:

ρₜ(x) ∝ lim(Ω→x) [N_front(Ω) / Δτ(Ω)]

This definition provides a direct interpretation that maps TDF's abstract computational "ticks" to SIT's physically measurable clock rate.

2. Coherence Magnitude (R_coh) from Front Regularity

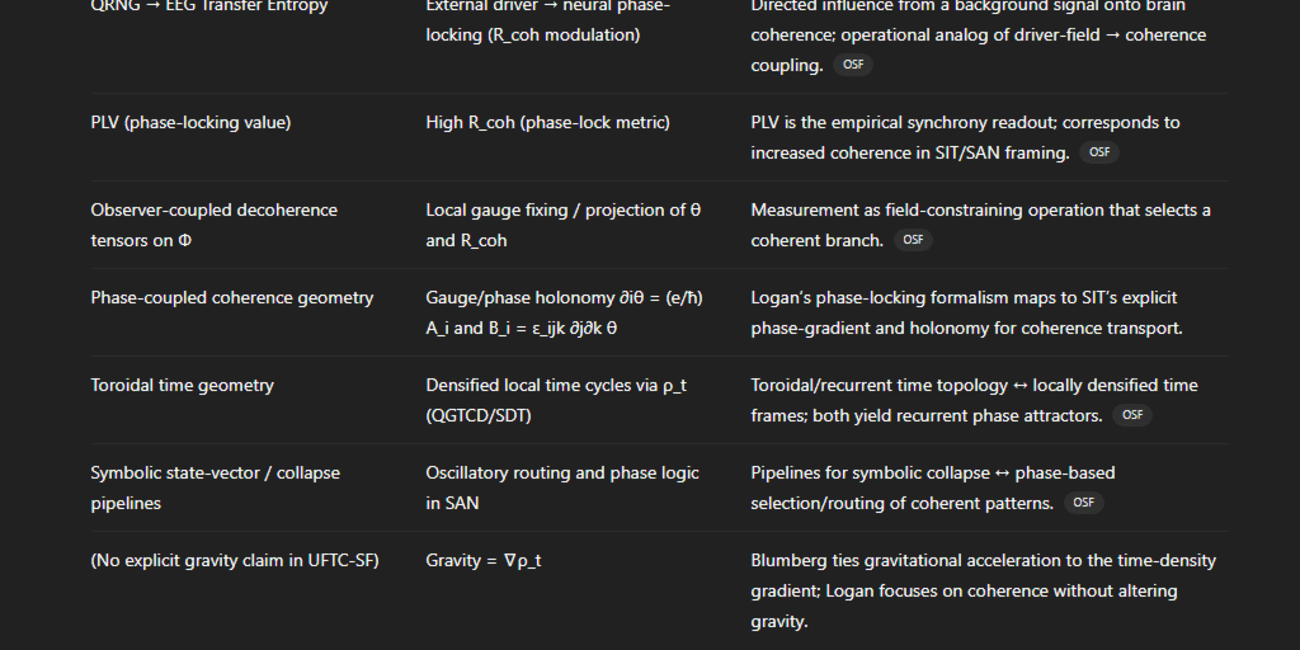
The SIT coherence ratio, R_coh(x), is constructed as a normalized local order parameter measuring the geometric regularity of the TDF front. Operationally, it quantifies the directional alignment and phase-locking of the front's constituent patches within a given window. A highly regular or aligned front corresponds to maximal coherence (R_coh → 1), whereas a chaotic or null front signifies decoherence (R_coh → 0). This maps the geometric order inherent in TDF's propagating structure directly to the informational order quantified by SIT's coherence field.

3. Phase (θ) and Gauge Connection (A_μ) from Front Geometry

The underlying U(1) gauge structure of SIT can be extracted from the geometry of the TDF front, Σ. By choosing a smooth parametrization of the front, we can define a phase field, θ(x), as the accumulated signed turning angle or isochronal phase (of a smooth parametrization of the TDF front Σ). From this, the SIT electromagnetic vector potential, A_μ(x), is defined by the gradient of this phase:

A_μ(x) := (ħ/e)∂_μθ(x)

This interpretation uncovers a hidden U(1) gauge structure within TDF's geometry, making a direct, falsifiable connection to electromagnetism and allowing for the recovery of physical phenomena such as Aharonov-Bohm holonomy from the front's topological properties.

4. Coherence Current (J_coh^μ) from Front Flux

The flow of information within the system is captured by defining the SIT coherence current, J_coh^μ, as the flux of the TDF front. With the front's normal propagation speed denoted by v_n and its unit normal vector by n^μ, the current is set as:

J_coh^μ ∝ R_coh · v_n · n^μ

This definition ensures that the channel along which information propagates in SIT corresponds directly to the propagation of the active boundary in TDF.

With the establishment of these definitions, and the calibration of a single constant to set the units, the complete map ⟦TDF⟧ = (ρₜ, R_coh, θ, J_coh) provides a full translation of any TDF history into the set of SIT's physical and measurable observables.

---

π-Calculus–Level Equivalence

A full proof would require formal LTSs and bisimulation. Conceptually, both are computational generators of physics (iterative recursion in TDF-0; dissipative computation/teleonomy in SIT). A simulation TDF-0 ⇒ SIT is straightforward at the level of shared observables (flows/energetics):

• Translation map (coarse-grained):
  ρₜ(x) ∝ lim_{Ω→x} N_front(Ω)/Δτ(Ω); R_coh from front alignment; θ from turning-angle/phase of front Σ; then A_μ := (ℏ/e)∂_μθ and define J_coh via front-flux. With one calibration, ⟦TDF⟧ = (ρₜ, R_coh, θ, J_coh).

• Separating context (Aharonov–Bohm). SIT predicts a gauge-invariant holonomy ∮ A·dl ≠ 0 even with vanishing local fields; TDF-0 (as written) does not specify a θ/U(1) bundle, so this barb is undefined. Thus simulation holds for shared barbs, but bisimulation is not established without augmenting TDF with an explicit phase connection.

The Distinguishing Test: Simulation vs Bisimulation

A formal comparison reveals that while any TDF process can be simulated by SIT, the two are not provably identical (bisimilar) because SIT defines observables not explicit in TDF.

• What matches (simulation): TDF front propagation speed/energy maps to SIT evolution of ρₜ and R_coh and to flux of J_coh. On these shared observables, a TDF run can be simulated by SIT.

• The Argument for Simulation (TDF ≼ SIT): The propagation of TDF's front, its speed, and its energy can be fully described by the evolution of the SIT fields (ρₜ, R_coh) and the flow of the coherence current J_coh. Observationally, a TDF simulation is indistinguishable from its SIT-translated image with respect to shared observables like energy and propagation speed.

• The Separating Context (Aharonov-Bohm Test): Consider an experiment that measures the gauge-invariant phase, ∮ A⋅dl, around a closed loop where the local fields are zero.

• Separating context (Aharonov–Bohm ring): Measure the gauge-invariant phase ∮ A·dl around a loop with vanishing local fields.

  • SIT: predicts a non-zero, quantized holonomy from θ (A_μ=(ℏ/e)·∂_μθ).

  • SIT Prediction: Predicts a non-zero, quantized holonomy determined by the phase θ. This observable "barb" fires.

  • TDF-0 (as written): no explicit θ/U(1) bundle is specified, so this observable is undefined.
    Conclusion: TDF-0 simulates a subset of SIT’s barbs; full bisimulation is unproven unless TDF-0 is augmented with an explicit phase connection.

  • TDF Limitation: As formulated, TDF has no explicit phase field θ or U(1) connection. It cannot predict a value for this observable without being augmented with the very gauge structure that SIT already contains.

• Simulation (TDF ≼ SIT): Propagation speed/energy of TDF fronts are reproducible by SIT fields (ρₜ, R_coh) and J_coh; observational equivalence holds on shared barbs.

• Separating Context (AB Ring): Measure ∮_C A·dl around a flux tube with null local fields. SIT predicts quantized holonomy from θ; TDF, absent an explicit θ/U(1), does not. Conclusion: TDF simulates a subset of SIT, but full equivalence is unproven without adding a phase bundle to TDF.

Conclusion: TDF can be seen as a simulation of a subset of SIT's dynamics. However, SIT exposes a gauge-holonomy observable that TDF does not specify, proving the two theories are not fully equivalent in their current forms.

---

Distinctives:

• SIT distinctives (earlier-dated): explicit primitives (R_coh, ρₜ), conserved coherence current and gauge holonomy A_μ = (ℏ/e)∂_μθ, plus concrete metrology/BEC predictions. The conserved Noether current for coherence, J_coh^μ. The derivation of the electromagnetic potential from gauge holonomy, A_μ = (ħ/e)∂_μθ. Specific, falsifiable predictions for metrology (atomic clock shifts, BEC gravity tests).

• TDF-0 distinctives: zero-import axioms, Ω_D scaling, D=2 repellor, Polyakov worldsheet with c=D from counts.

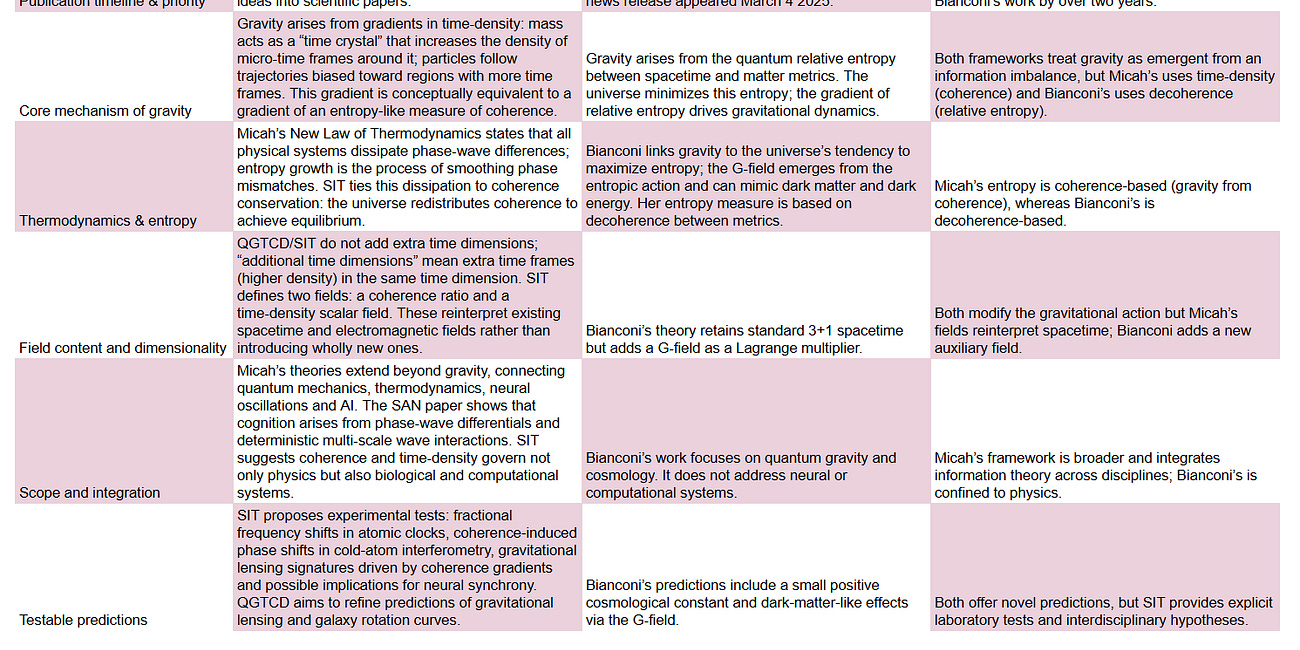
Given the records now online, Blumberg’s SDT (Jan 27, 2025) and SIT (Feb 9, 2025; updated Aug 2025) predate the posted TDF-0 materials (Aug 10, 2025). This supports a priority claim for SIT’s specific informational primitives and gauge-holonomy mechanism. As for intent, we cannot infer it from timestamps alone; the safest characterization is significant conceptual convergence with overlapping claims of emergence. Figshare+1 Zenodo

---

Timeline and Precedence

• Micah Blumberg: The provided documents indicate that Blumberg's work on Quantum Gradient Time Crystal Dilation (QGTCD), the precursor to SIT, was published in 2022 & in a series of articles on SVGN.io in 2024-2025.

• Super Dark Time (SDT). Figshare record indicates public posting on Jan 27, 2025 (DOI 10.6084/m9.figshare.28284545). Figshare

• Super Information Theory (SIT). Original Publication Date Feb 9, 2025; later drafts in early August 2025; record page present. Figshare+2Figshare+2

• Thompson Dimensional Framework (TDF) TDF-0 ⇒ TDF. Zenodo records published Aug 10, 2025 (records 16787848 and 16787944). Zenodo+1

The date stamps establish that Blumberg's SIT framework, including its specific physical fields and gauge-theoretic structure, was documented prior to Thompson's TDF.

---

Executive Summary

The conceptual and mathematical overlap between Thompson's “Thompson Dimensional Framework Origin (TDF-0),” with the work of Micah Blumberg, particularly Super Information Theory is overwhelmingly significant. Core TDF principles—such as a "zero-import" origin, worldsheet emergence from counts, and an arithmetic sector—are not only present in SIT but are given concrete, physical, and falsifiable forms that predate TDF's publication.

Both pursue “physics from scratch,” deriving sector laws and effective constants from a single generative mechanism, and connect counts/structure to actions and geometry. The translation map above shows how TDF-0 observables can be embedded in SIT’s operational fields, while the AB-holonomy test marks a current point of divergence. Based on publicly visible timestamps, SIT’s specific informational primitives and gauge-holonomy mechanism were documented earlier.

Therefore, TDF does not appear to be a novel theory but rather a re-articulation of the core generative logic of SIT, without the specific, physically grounded, and testable mechanisms that define the latter.

The similarities in core concepts, generative mechanisms, and claimed outcomes are substantial and consistent with possible intellectual inspiration. This article makes no claim about intent or misconduct; it documents overlap and precedence in the public record and invites further technical clarification or replication studies. We do not speculate about intent; our claim is limited to demonstrating significant conceptual convergence and documenting the earlier public record of SIT.

---